3.1. Mathematical Model

We shall model this problem in the following way. The network of pipes corresponds to a directed graph \(G = (V,A)\). Each arc \((v,w) \in A\) has specified capacity \(u(v,w)\). There is a specified source node \(s \in V\) (where the flow comes from) and a specified sink node \(t \in V\) (where the flow goes to). This is the entire input to the maximum flow problem.

To specify a solution for this input, we must give a flow value \(f(v,w)\) for each arc \((v,w) \in A\). Such a solution \(f\) is feasible if

1. \(0 \leq f(v,w) \leq u(v,w)\) for each \((v,w) \in A\); and

2. \(\displaystyle{\sum_{(w,v)\in E} f(w,v) = \sum_{(v,w)\in E} f(v,w)}\) for each node \(v \in V \setminus \{s,t\}\) (i.e., for each node that is neither the source nor the sink).

The first type of constraints, the inequalities, are called capacity constraints; and the second type, the equations, are called node flow conservation constraints.

The value of a flow \(f\) is the total net flow into \(t\), which is equal to

\[\sum_{(w,t) \in A} f(w,t) - \sum_{(t,w)\in A} f(t,w).\]

This is the objective function for the maximum flow problem; in other words, we wish to find a feasible flow of maximum value.

Maximum flow problem

input:

• directed graph \(G=(V,A)\),

• a source node \(s \in V\), a sink node \(t\in V\), and

• a nonnegative capacity \(u(v,w)\) for each arc \((v,w)\in A\)

output:

• a flow value \(f(v,w)\) for each arc \((v,w)\in A\) so that

  1. \(0 \leq f(v,w) \leq u(v,w)\) for each \((v,w) \in A\); and

  2. \(\displaystyle{\sum_{(w,v)\in A} f(w,v) = \sum_{(v,w)\in A} f(v,w)}\) for each node \(v \in V \setminus \{s,t\}\)

goal: maximize the net flow into the sink node, i.e.,

\[\text{maximize} \sum_{(w,t) \in A} f(w,t) - \sum_{(t,w)\in A} f(t,w)\]

Q: Do you understand the difference between a flow and the value of a flow?

Example

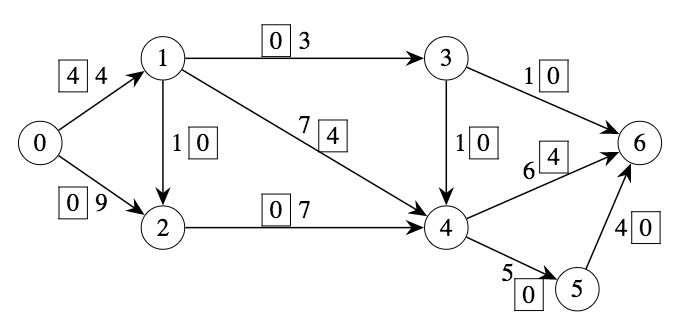
Consider the following instance. The numbers on the arcs are the capacities.

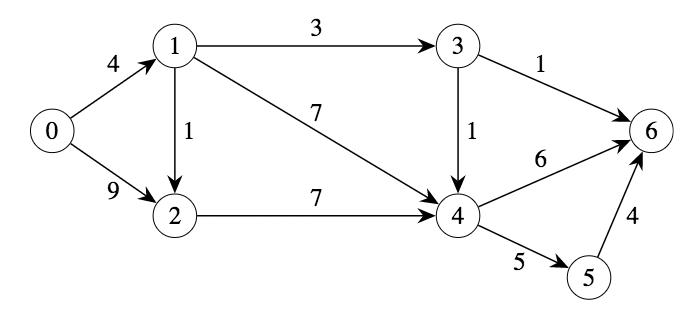
Q: Which nodes are the source and sink? What is \(u(1,4)\)?

A: Node 0 is the source since it has no incoming arcs while node 6 is the sink since it has no outgoing arcs. \(u(1,4) = 7\).

We would like to push as much flow as we can from node 0 to node 6. Say we pick the path 0-1-4-6.

Q: How many units of flow can be pushed through this path?

Q: Is there an arc which got saturated (that is, no more flow can go through it)?

Now, we write down the flow on the arcs (number inside a box).