2. The Shortest Path Problem

Consider the following problem. You are given a map of the city in which you live, and you wish to figure out the fastest route to travel from your home to your office. In your city, some of the streets are two-way, and some are one-way. Furthermore, traveling down a street in one direction might not take the same time as in the other direction (e.g., if there is some construction taking place on your side of the street). Figures 2.1 and 2.2 below show how you might choose to model this type of problem on a graph.

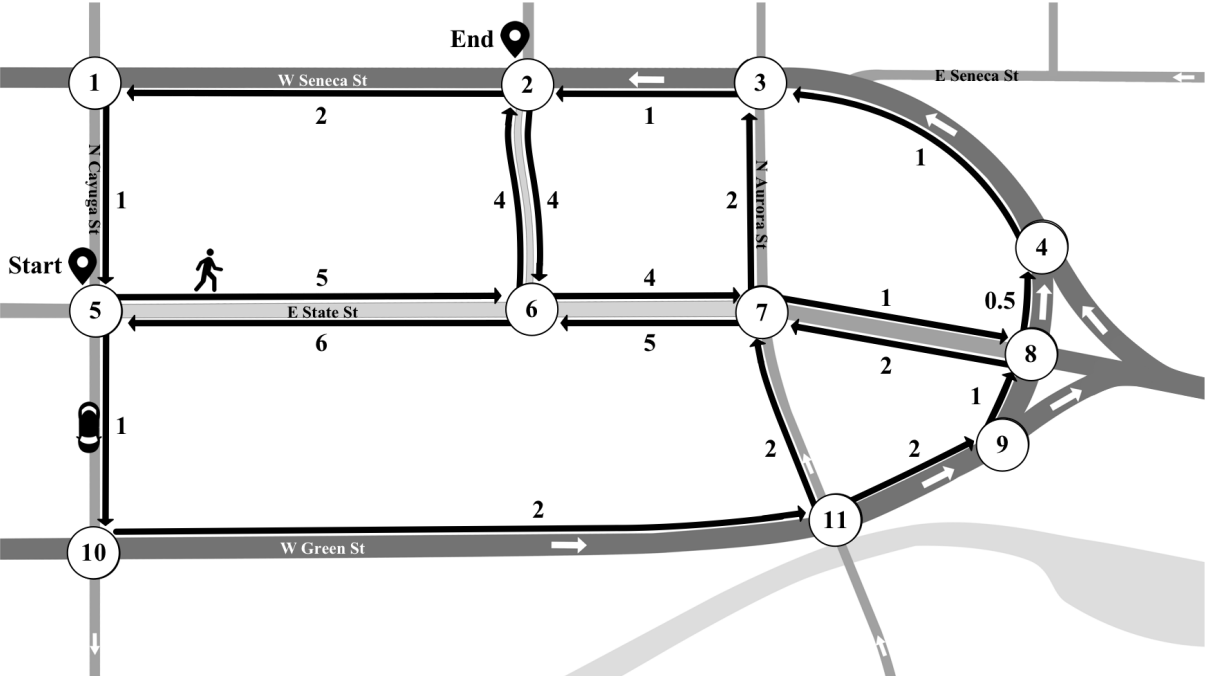
Fig. 2.1 A map of the Ithaca Commons

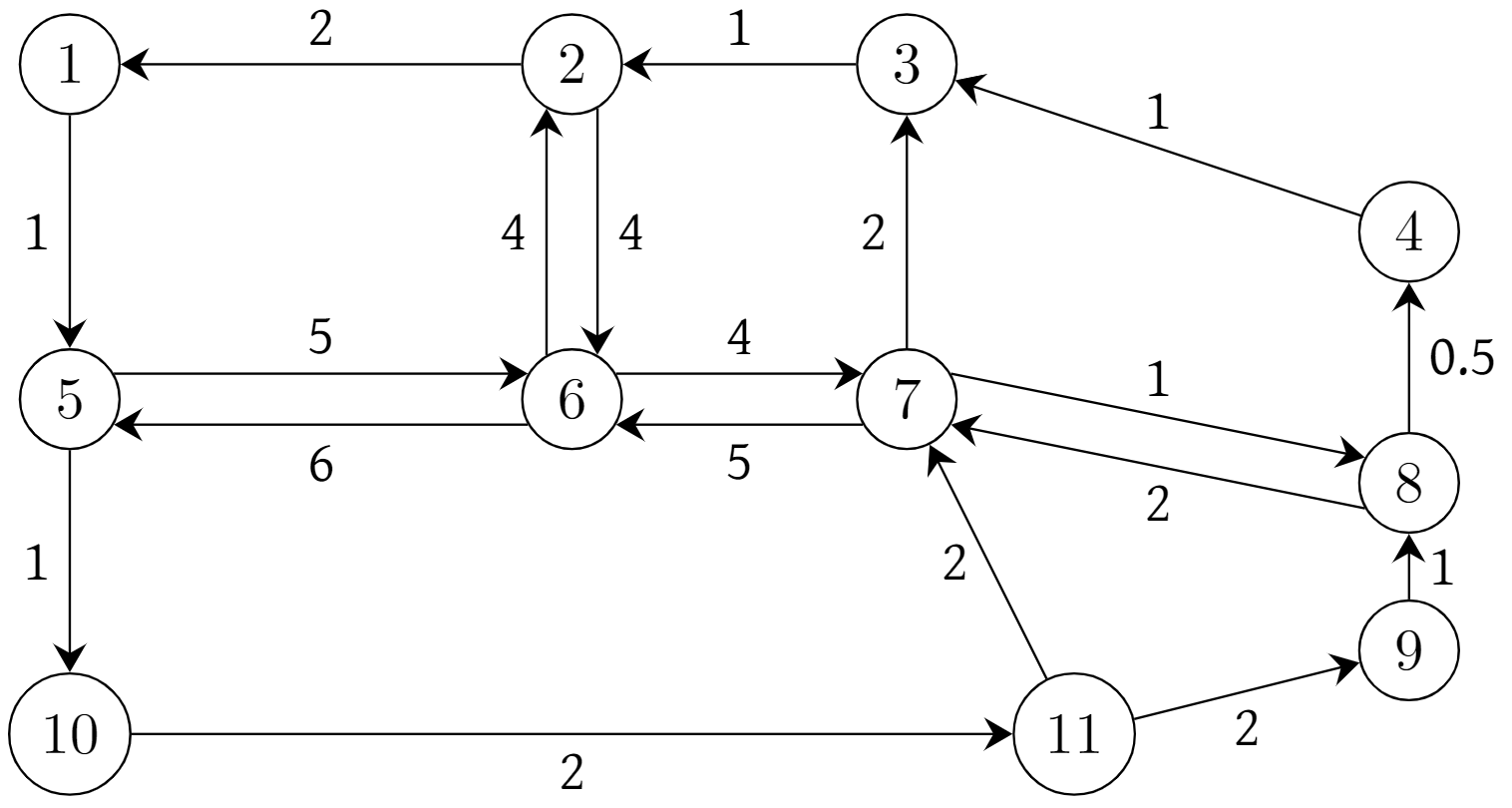
Fig. 2.2 A directed graph modeling the situation in Figure 2.1

First of all, we would like to give a mathematical model of this problem. To do this, it will be useful to introduce the notion of a directed graph. A directed graph consists of a set of nodes and a set of arcs. For example, Figure 2.3 below shows a graph in which 1, 2, 3, 4, 5, and 6 are the nodes of the graph. That is, in drawing a graph we represent a node by a circle with its name indicated inside. An arc is an ordered pair of nodes, such as \((1,2)\). The arc \((1,2)\) is represented below as the arrow that points from node 1 to node 2, hence “directed”. For nodes 2 and 3, there is an arc from 2 to 3 and an arc from 3 to 2. Thus, if we consider the graph below, then the set of nodes is \(\{1,2,3,4,5,6\}\), and the set of arcs is

\[\{(1,2), (1,3), (2,3), (2,4), (3,2), (3,5), (4,3), (4,6), (5,2), (5,6) \} .\]

We let \(N\) be the name for the set of nodes, that is, \(N=\{1,2,3,4,5,6\}\), and we let \(A\) be the name for the set of arcs:

\[A= \{(1,2), (1,3), (2,3), (2,4), (3,2), (3,5), (4,3), (4,6), (5,2), (5,6) \} .\]

When we specify the elements that are contained in a set, it does not matter in which order we list them. For example, we could equally well have described \(N\) as \(\{ 1, 3, 4, 6, 5, 2\}\) since it is the same set. If we call the graph \(G\), then we often write \(G=(N,A)\) to mean that \(N\) is its set of nodes, and \(A\) is its set of arcs.

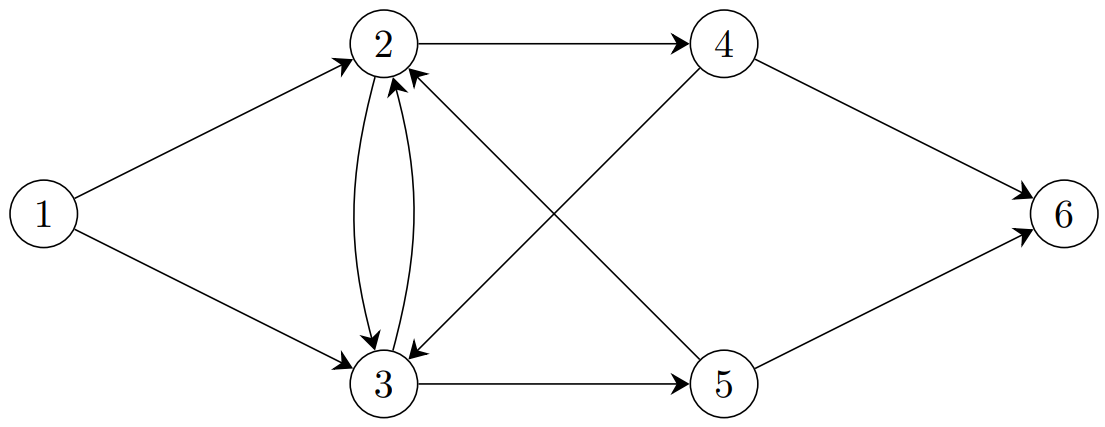
Fig. 2.3 A graph with 6 nodes and 10 arcs

A path in a graph is a sequence of arcs that, from a visual perspective, you could follow with your pencil without lifting it up. For example, \((2,3), (3,5), (5,6)\) is a path from node 2 to node 6 in the graph given in Figure 2.3. There are two important things to notice. First, a path is a sequence of arcs, not a set of arcs: the order in which we list the arcs does matter. Second, we are following each arc in its given direction. For example, \((3,2),(2,1)\) is not a path from node 3 to node 1 because there is no arc \((2,1)\) in the graph in Figure 2.3; only \((1,2)\) is an arc in this graph. In general, we can write a path as follows: let \(i_1\), \(i_2\), \(\ldots\), \(i_k\) denote nodes in the graph (not necessarily the nodes \(1,2,\ldots,k\)); then

\[(i_1,i_2), (i_2,i_3), (i_3,i_4) ,\ldots, (i_{k-1},i_k)\]

is a path in the graph from node \(i_1\) to node \(i_k\) provided that each of \((i_1,i_2)\), \((i_2,i_3)\) through \((i_{k-1},i_k)\) is an arc in the graph. This path has \(k-1\) arcs in it.

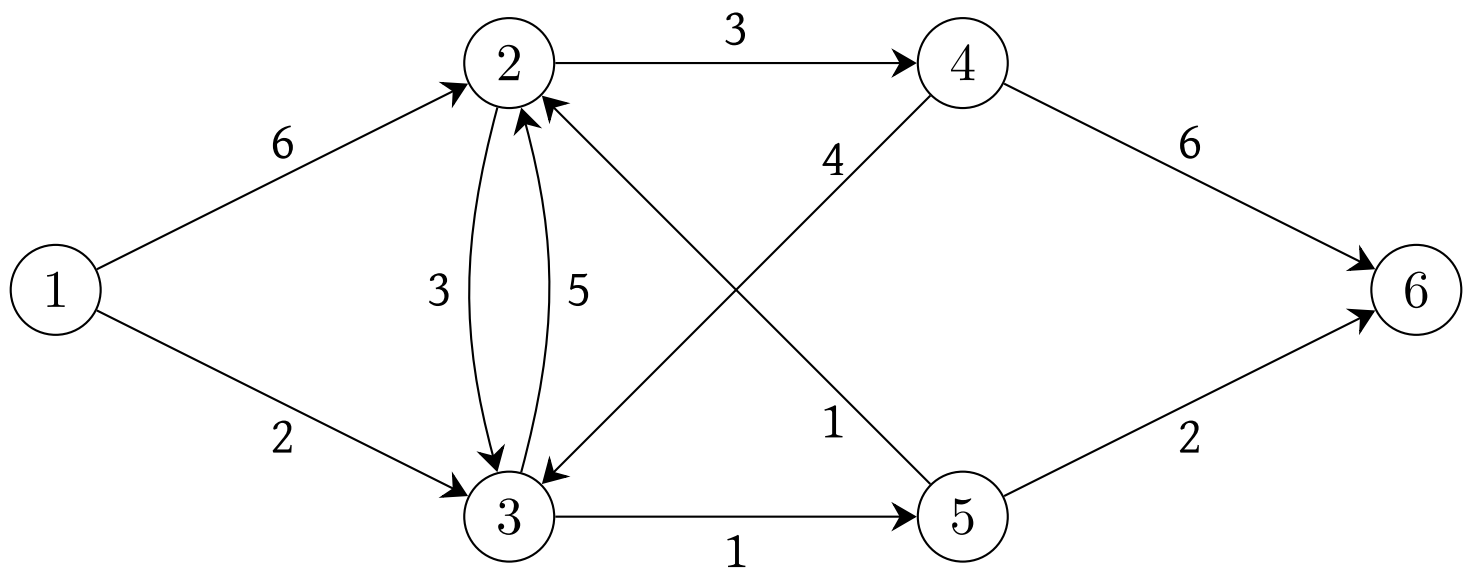
Fig. 2.4 A graph with arc lengths

We will often be interested in directed graphs for which each arc has an associated length. We will denote the length of each arc \((i,j)\) in \(A\) by \(\ell(i,j)\). In the graph in Figure 2.4, we have added lengths by writing each arc’s length right next to it. For example, the length of arc \((3,2)\) is 5, or equivalently, \(\ell(3,2)=5\). The length of a path is the sum of the lengths of the arcs in it. For example, the path from node 2 to node 6 given by \((2,3), (3,5), (5,6)\) has length equal to \(3 + 1 + 2 = 6\). In this graph, there are two paths from node 2 to node 6 of length 6. Can you find the other one? We will be interested in finding the shortest path between a given pair of nodes. This is the next optimization model that we shall consider in this course.