1. The Traveling Salesman Problem

The traveling salesman problem, or TSP, is one of the most notorious optimization problems. The setting for the problem is as follows. A salesman starts at his home and has a given set of cities to visit. That is, if his home is in New York, and he must visit Syracuse, Chicago, San Francisco, Los Angeles, Detroit, and Atlanta, then one possible solution is to go from New York to Chicago to San Francisco to Los Angeles to Detroit to Atlanta to Syracuse, and then to return home to New York. Given that he is traveling to many cities and not staying over a Saturday night, he only qualifies for the standard coach airfare between each consecutive pair of cities that he visits. He knows the airfare between each pair of cities. That is, in our example, he might be given the following table of airfares:

	NY	Syracuse	Chicago	SF	LA	Detroit	Atlanta
NY	—	202	135	245	245	169	129
Syracuse	202	—	309	445	445	230	160
Chicago	135	309	—	180	180	105	120
SF	245	445	180	—	39	195	165
LA	245	445	180	39	—	195	165
Detroit	169	230	105	195	195	—	135
Atlanta	129	160	120	165	165	135	—

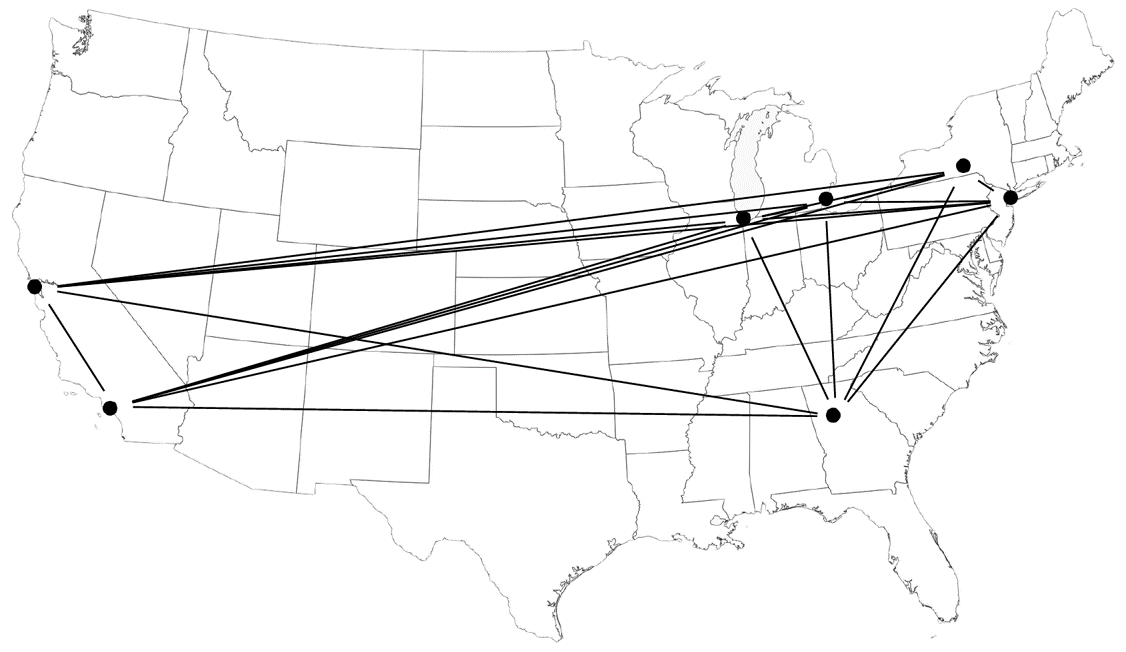
Fig. 1.1 A visualization of the traveling salesman problem

Notice that the data contain a few irregularities (common to the airline industry). The airfare from Syracuse to San Francisco is \(445\), but the airfare from Syracuse to Atlanta is \(160\) and the airfare from Atlanta to San Francisco is \(165\), for a total fare of \(325\). Unlike in this case, if the table of fares has the property that the cheapest way to go between each pair of cities is to take the non-stop flight, then the fares are said to satisfy the triangle inequality. In cases such as the one above, they are said to violate the triangle inequality. We shall assume that the salesman is pressed for time and always takes the non-stop flight between each of his stops on his tour. Thus, the cost of the tour proposed above is:

\[135 + 180 + 39 + 195 + 135 + 160 + 202 = 1046.\]

Alternatively, if he were to go from NY to Syracuse to SF to LA to Chicago to Detroit to Atlanta to NY, then the cost would be

\[202 + 445 + 39 + 180 + 105 + 135 + 129 = 1235.\]

Clearly, the first tour is better. The salesman would like to choose the order in which to visit the cities so as to minimize the total cost of his trip. For the data given above, is the first proposed tour the cheapest one?

The traveling salesman problem is an optimization problem. For any optimization problem, there is some notion of what kind of input is expected. For the traveling salesman problem, the input consists of a table of costs, such as the one given above, and it could involve any number of cities. For any optimization problem, there is also a notion of a feasible solution; that is, a possible answer (though not necessarily the best answer). For this problem, a feasible solution is a tour that visits all of the cities and returns to the starting point. And finally, there is the notion of an objective function — the criterion by which we choose which of the feasible solutions is the best one, the optimal solution. In this case, the objective function is the sum of the costs of flying between each pair of cities that occur consecutively in the tour, and we want to minimize the value associated with the feasible solution. In other problems, we could be dealing with a maximization.